What is a Constant Phase Element?
The Constant Phase Element (CPE) is a non-intuitive circuit element that was discovered (or invented) while looking at the response of real-world systems. In some systems the Nyquist plot (also called the Cole-Cole plot or Complex Impedance Plane plot) was expected to be a semicircle with the center on the x-axis. However, the observed plot was indeed the arc of a circle, but with the center some distance below the x-axis.
These depressed semicircles have been explained by a number of phenomena, depending on the nature of the system being investigated. However, the common thread among these explanations is that some property of the system is not homogeneous or that there is some distribution (dispersion) of the value of some physical property of the system.
CPE equations
Mathematically, a CPE’s impedance is given by
1 / Z = Y = Q° ( j omega )n
where Q° has the numerical value of the admittance (1/ |Z|) at omega =1 rad/s. The units of Q° are S•sn (ref 1).
A consequence of this simple equation is that the phase angle of the CPE impedance is independent of the frequency and has a value of -(90*n) degrees. This gives the CPE its name.
When n=1, this is the same equation as that for the impedance of a capacitor, where Q° =C.
1 / Z = Y = j omega Q° = j omega C
When n is close to 1.0, the CPE resembles a capacitor, but the phase angle is not 90°. It is constant and somewhat less than 90° at all frequencies. In some cases, the ‘true’ capacitance can be calculated from Q° and n
The Nyquist (Complex Impedance Plane) Plot of a CPE is a simple one. For a solitary CPE (symbolized here by Q), it is just a straight line which makes an angle of (n*90°) with the x-axis as shown in pink in the Figure. The plot for a resistor (symbolized by R) in parallel with a CPE is shown in green. In this case the center of the semicircle is depressed by an angle of (1-n)*90°
What Causes a CPE?
| In his textbook, Macdonald ( Ref 1 ) points out that even though a particular theory may not give exactly CPE behavior, very often CPE behavior will fit experimental data so well that the deviations are totally masked by experimental noise and uncertainties. This is increasingly true as the complexity of a circuit model grows. In short, a CPE can provide a useful modeling element, even if the true nature of the system is unknown. |
Surface Roughness
One physical explanation put forth for CPE behavior is electrode roughness. For a rough, fractal, surface, the fractal dimension (D) of the surface is between 2 and 3: Translated, this means that the surface fills between 2 dimensions (i.e., it’s absolutely flat) and 3 dimensions (i.e., the surface fills three dimensions, branching every-which-way through space, and resembling a porous cube.) It has been shown ( Ref 2 ) that for these electrodes, the interfacial impedance (electron transfer or double layer capacitance) is modified by an exponent, n = 1/(D-1). For a smooth surface the fractal dimension (D) is 2.0 and n=1: The impedance is unchanged. For a highly contorted surface (D=3), and n=0.5.
For a great many real metal or solid electrodes, the measured impedance in the double-layer region (no faradaic current) follows a power law, such as that for the CPE, with a value of n between 0.9 and 1.0. The phase angle of this “capacitance” is not 90° , but is given by (n*90°). The observed angle is something between 80° (n=0.89) and 90° (n=1.0). When this “capacitance” is in parallel with a charge-transfer resistance (R), the Nyquist plot is the arc of a circle, but with the center of the circle blow the x-axis: It is the “depressed semi-circle” shown in the figure on the previous page. This behavior is not seen on a mercury electrode because, as a liquid, it is atomically smooth!
A Distribution of Reaction Rates
Another explanation is inhomogeneous reaction rates on a surface. This might be seen at polycrystalline metal surfaces or carbon electrodes with a distribution of active sites (with varying activation energies) on the surface. A recent article ( Ref 3 ) shows that for a glassy carbon electrode, the CPE exponent correlates with the fraction of exposed edge plane orientation, not with the fractal dimension of the surface. Mercury, which does not show CPE behavior, is also atomically homogeneous, unlike polycrystalline metals.
This explanation is explored further in the discussion of the ZARC circuit element
Varying Thickness or Composition
A third possible explanation may be varying thickness or composition of a coating. For example, if the bulk conductivity of a coating changes with distance through the coating (see Ref 4), then the resultant impedance spectrum can closely approximate that of a CPE.
Non-uniform Current Distribution
At the 2004 EIS Symposium, Tribollet ( Ref 5 ) presented a paper in which he looked at the EIS of a Mg alloy in dilute Na2SO4. The impedance of the whole electrode was measured in the traditional way and the spectrum above 1 Hz was fit to a Randles Cell containing a CPE with an n-value of 0.91.
The local impedance was also measured by placing a sub-mm current probe a short distance over the electrode. The local impedance was measured as a function of the distance along the radius of the electrode. Near the center, the n-value for the CPE was 1.0, indicating a true capacitance. However, at the edge of the electrode, the n-value for the CPE was 0.83! We would expect the current density to be fairly homogeneous near the center of the electrode, and normal to the surface. Near the edge, the current density will certainly be perturbed by “edge effects.” Current flow will also not be perfectly normal to the surface. Both effects are likely to change the n-value for the CPE.
Another publication “The RC time ‘constant’ at a disk electrode” ( Ref 6 ) discusses the same phenomenon, but from a slightly different perspective. Oldham showed that the local RC time constant (uncompensated- or solution-resistance times double layer capacitance) varies from 0 to 2RC over the disk.
The CPE – Calculating Capacitance from Q°
What is the TRUE Capacitance?
If the n-value of a CPE is a little less than 1.0, then the CPE behavior is close to that of a capacitance. Many researchers wish to calculate the “correct” capacitance corresponding to the Q° value of the CPE. The similarity of the equations makes it inviting.
CPE 1 / Z = Y = Q° ( j omega )n
Capacitor 1 / Z = Y = Q° ( j omega )1 = C ( j omega )
where Q° is numerically equal to the admittance (1/ |Z|) at omega =1 rad/s. It is tempting to simply associate the value of Q° for a CPE with the capacitance value, C, for an equivalent capacitor. Alas, an examination of the units of C (farad or S-s ) and Q° ( S-sn ) shows that they can not be the same! See ref 1 for unit abbreviations.
For the case of a ‘classical’ depressed semicircle (CPE in parallel with a resistance) Hsu and Mansfeld (ref 2) have given this equation for calculating the ‘true’ capacitance, C:
C = Q° ( omegaMAX )n-1
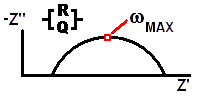 In this equation, omega max represents the frequency at which the imaginary component reaches a maximum. It is the frequency at the top of the depressed semicircle, and it is also the frequency at which the real part ( Z’ ) is midway between the low and high frequency x-axis intercepts.
In this equation, omega max represents the frequency at which the imaginary component reaches a maximum. It is the frequency at the top of the depressed semicircle, and it is also the frequency at which the real part ( Z’ ) is midway between the low and high frequency x-axis intercepts.
| The equation proposed by Hsu and Mansfeld is based on the model of a CPE in parallel with a charge transfer resistance. MAX may not even exist for other circuits, such as a CPE and a resistor in series! |
REFERENCES
(1) “Impedance Spectroscopy“, JR Macdonald, ed., John Wiley, 1987. Sect. 2.2.3.4.
(2) “Tafel current at fractal electrodes. Connection with admittance spectra,” WH Mulder, JH Sluyters, T Pajkossy, I Nyikos, J. Electroanal. Chem., 285 (1990) 103.
(3) “An investigation of the capacitance dispersion on the fractal carbon electrode with edge and basal orientations,” C-H Kim, S-I Pyun, J-H Kim, Electrochimica Acta, 48 (2003) 3455.
(4) “The evaluation of experimental dielectric data of barrier coatings by means of different models,” CA Schiller, W Strunz, Electrochimica Acta, 46 (2001) 3619.
(5) “CPE Analysis by Local Impedance Analysis”, J-B Jorcin, ME Orazem, N Pebere, B Tribollet, Electrochimica Acta, 51 (2006) 1473-1479. Paper presented at EIS Symposium, Coco Beach, FL, June 2004.
(6) “The RC time ‘constant’ at a disk electrode”, KB Oldham, Electrochem. Communications, 6 (2004) 210-214.
