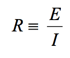Fitting EIS Data – Diffusion Elements
Whenever you look at a Complex-Plane Impedance Plot ( Nyquist or Cole-Cole plot) and see a 45° line, or fit data to an equivalent circuit and find a Constant Phase Element (CPE) with an n-value close to 0.5, you should consider diffusion as a possible explanation.
Diffusion Circuit Elements – Warburg
The most common diffusion circuit is the so-called “Warburg” diffusion element, but it is not the only one! A Warburg impedance element can be used to model semi-infinite linear diffusion, that is, unrestricted diffusion to a large planar electrode. This is the simplest diffusion situation because it is only the linear distance from the electrode that matters.
The Warburg impedance is an example of a constant phase element for which the phase angle is a constant 45° and independent of frequency. The magnitude of the Warburg impedance is inversely proportional to the square root of the frequency
![]() as you would expect for a CPE with an n-value of 0.5. The Warburg is unique among CPE’s because the real and imaginary components are equal at all frequencies and both depend upon
as you would expect for a CPE with an n-value of 0.5. The Warburg is unique among CPE’s because the real and imaginary components are equal at all frequencies and both depend upon ![]()
[…]

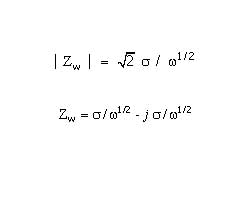
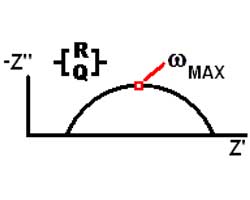

 One guideline that I have heard recommended (although I cannot give a reference for it) is that data over a decade range of frequency is required to support each circuit component.
One guideline that I have heard recommended (although I cannot give a reference for it) is that data over a decade range of frequency is required to support each circuit component.